Abstract
At the core of any artificial intelligence project is the need to find the simplest yet most efficient solution to any given problem. The evolved perceptron is yet another attempt to do this. It applies a basic evolutionary concept to hopefully help the perceptron learn better and more efficiently. In other words, the evolved perceptron is an attempt to merge a multilayer perceptron based learning model and a basic neuroevolutionary approach to machine learning. In this paper, we will discuss the algorithm behind the evolved perceptron, whether it makes perceptron based learning better and whether it is more efficient. After which, we will look at a parallelized version of it and determine whether or not it is worth parallelizing, some things to consider when doing so, and what may be the best approach to its parallelization.
Introduction
Recognition and categorization are both in their own right, important aspects for research & development in this time and era. Hence exploiting the accessible techniques in Artificial Intelligence (AI) and using said techniques to create new ones are key. In the AI field multilayer perceptrons(MLP) are categorized under the artificial neural networks(ANN) and within that, it is considered to be a form of supervised learning. This project came to be from a matter of interest in improving the perceptron model of learning, a basic understanding of neuroevolution and a love for parallelization.
In the past few years, there has been a renewed interest in perceptrons for machine learning. Hence the purpose of this paper is not only to introduce a somewhat novel idea for a modified version of the multilayer perceptron but it is also to introduce possible parallel techniques for this version of the multilayer perceptron.
The success of this project can be viewed in two parts; does it learn better? And does it learn faster? This paper will attempt to show that the evolved perceptron learns better and faster than an average multilayer perceptron. In this paper we will start by first discussing the details involved in the implementation of both the parallel and sequential version of it in comparison to an implementation of a regular multilayer perceptron, so as to show that there is no bias in any of the implementations. After which, the design of the experiment to show the evolved perceptron is truly better, will also be discussed along with the results of the experiments in great detail. However we will begin by giving the necessary background needed to understand the rest of this paper, although some prior knowledge of machine learning is assumed.
Background
An Artificial neural networks can be defined as a computational model based on the nervous system [Alsmadi et al., 2009]. It is based on the neural structure of the brain. The brain learns from expe-rience, hence it is the goal of artificial neural networks to mimic this. It does so by trying to mimic the mechanics involved in how the brain processes information, using the neurons and thus be able to solve a range of problems. Within this is a subset of algorithms regarded as supervised learning. This is a method of machine learning where the desired output is given and it is up to the machine to come up with a function that captivates the desired output.
The invention of perceptrons date back to the 1950s, it was one of the first artificial neural network ever to be produced [Wikipedia, 2004]. Perceptrons fall under the supervised learning category. It is an algorithm for learning binary classifiers (categorization). It creates a function that can determine whether or not a given set of inputs belong to one category or another. A multilayer perceptron (MLP) on the other hand is an artificial neural network that is comprised of many neurons, divided up into several layers [Karapetsas, 2009a]. An MLP does the same things as a regular perceptron but significantly better. This concept is quite different from the neuroevolution approach to machine learning.
Neuroevolution on the other hand is a machine learning technique that uses evolutionary algorithms to construct artificial neural networks. It takes its inspiration from the evolution of biological nervous systems in nature. Compared to perceptrons, neuroevolution is highly general; it allows learning without explicit target and it can be used for both supervised and unsupervised learning models. Neuroevolution is a good approach to applying reinforcement learning. It is most commonly applied in evolutionary robotics and artificial life[Lehman and Miikkulainen, 2013].
The concepts applied in the evolved perceptron is heavily bias towards the multilayer perceptron. It uses all the key concepts from a regular MLP such as: activation and back propagation. However it takes only one key concept from neuroevolution—survival of the fittest. So in a sense, it evolves to use only the things it deems as important to the learning process, discards of the weakest links and replaces them with duplicates of the known bests in the network. Note that, from here on out I will use the phrases: evolved MLP and evolved perceptron interchangeably to refer to the algorithm which is the purpose of this paper.
Methodology
For the evolved perceptron, first an implementation of a regular MLP was first designed. This particular implementation used is a 2-layered perceptron, however this can be implemented in many number of ways. The regular MLP learns linear equations and was tested and trained based on random inputs between 5 and -5. This range was chosen because it sped up learning a lot as opposed to looking at an infinite range of numbers. My inputs were random numbers generated between 0 and 1 with a precision of six decimal places. Having inputs between 0 and 1 gives a lot more control to the weights in terms of how the output is determined. The step value used was 10 and it seemed to give the best results in both speed and better learning. The sigmoid function is used for back propagation and updating the weights after the prediction error of a given node has been determined. After the sequential MLP was designed it was then modified to include the survival of the fittest concept, this was initially done, by simply removing the worst after every pass and replacing it with one of the best, however this made the learning process substantially slower and often did not learn at all. The algorithm was then reconstructed to only replace the worst when the difference between the worst and the best was greater than 0.12. This value was not selected randomly it was gotten from running several tests and finding the best number. It was the best number that allowed the worst the network a chance to learn (become more fit) and did not sacrifice too much of time/speed. Another factor that determined whether or not it was time to replace the worst was when the last worst was replaced, if it was replaced more than five passes ago then the current worse can be replaced otherwise, it gives the current worst some time to still learn. Five as well was not randomly selected but was chosen as the best from several tests with input and hidden node sizes ranging from 5 to 10,000. Replace worst works in such a way that it randomly selects from the best two which one to replace the worst hidden node with.
In the parallel version, threads are used as opposed to processes, this decision was not overly thought out, but was done to see how it would perform. The number of threads created equal the number of processors the running computer has. This is to increase the probability of true concurrency. Each thread worked on a calculated subset of hidden nodes. However, if the number of nodes is not evenly divisible by the number of processors without a remainder we then have what i term to be overloaded thread. This thread does more work than the others, calculating the hidden nodes that could not be assigned to any of the other processes. My first try at a parallel algorithm created and deleted threads as they were needed, creating threads when back propagation needed to be done and deleting them right after they were done their assigned work. This led to a ludicrous overhead but required less synchronization overall. My second attempt, created threads and deleted them per training session (threads are created once and deleted once all training samples have been exhausted), this was better than the former implementation because we were only training for one classifier the whole time. However, as soon as the test suite was added, where we had 100 classifiers to work with, the overhead of creating and deleting the threads skyrocketed. For instance, if we were to have 50 training set for the network to learn a given classifier and 1,000 test samples afterwards, when I add in my test suite we would then have 100,000 testing samples across all classifiers and 5,000 training sets in total and if the number of processors is 4 we would have then created and deleted 400 threads. After noticing this, I rewrote the parallel algorithm to create and delete threads threads only once. It creates them as soon as the program starts running and uses them across training for all classifiers. No parallelization was done for testing the perceptron on each classifier however, this may speed up the algorithm. I deemed it unnecessary because it will not speed it up by enough to justify its parallelization. This leads me to believe that, the best way to parallelize this is in such a way that threads are created and deleted only once the entire time the program is running.
Experiment Settings
After the sequential and parallel version of the evolved MLP were designed and tested, they were then compared to the original sequential MLP. To ensure that the values gotten from the tests were an accurate representation of how they perform against each other, the test suite discussed above, was designed to generate only one set of random values for inputs and training, this is then stored in a file and used by all three versions (regular MLP, serial evolved perceptron and parallel evolved perceptron) of the MLP when run. However the inputs used to test each classifier remained random. 5 test suites were generated each testing one hundred classifiers, but each test suite has different input and hidden node sizes. Test suite 1 is for 5 input weights, 4 hidden nodes and 20 training sets, test suite 2 is for 50 input weights, 40 hidden nodes and 200 training sets, test suite 3 is for 100 input nodes, 90 hidden nodes and 500 training sets, test suite 4 is for 500 input weights, 452 hidden nodes and 1000 training sets, and test suite 5 is for 1000 input nodes, 952 hidden nodes and 1500 training sets. These algorithms were compared on two fronts; time taken and success rates per classifier. The success rates were put into groups such as 90-100, 80-89 and so on. More test suites can be created by simply changing the appropriate values in the test suite generator. Note that,these tests were run on a 4 core machine running Mac OSX 10.11, hence processing power was somewhat limited for these tests. When timed, the time taken for all versions included time it took to read in the data from the file, and in the case of the parallel version it also included time taken to create and destroy all threads.
Results & Discussion
Tables 1,2,3,4 and 5 are tables that show the accuracy results from each test suite. Note that, for each test suite each MLP version is tested with 100 classifiers. Each column holds the accuracy results after testing how well the perceptron learns 1,000 times with truly random inputs. The summation of all cells in a given column will equal 100 which is the number of classifiers. The number in each cell of a single column, represents the number of times the MLP was able to learn the classifier enough to produce a success rate within the given range highlighted on the leftmost column. Table 6 shows the time taken to run each test suite.
| Accuracy % | Regular MLP | Serial Evolved MLP | Parallel Evolved MLP |
|---|---|---|---|
| 90-100 | 46 | 46 | 48 |
| 80-89 | 16 | 15 | 11 |
| 70-79 | 13 | 13 | 10 |
| 60-69 | 9 | 10 | 15 |
| 50-59 | 11 | 9 | 6 |
| 40-49 | 0 | 1 | 2 |
| 30-39 | 5 | 6 | 5 |
| 20-29 | 0 | 0 | 0 |
| 10-19 | 0 | 0 | 0 |
| 0-9 | 0 | 0 | 0 |
Table 1: Test Suite 1 (4 Hidden Nodes, 5 Input Nodes)
| Accuracy % | Regular MLP | Serial Evolved MLP | Parallel Evolved MLP |
|---|---|---|---|
| 90-100 | 37 | 38 | 37 |
| 80-89 | 12 | 12 | 13 |
| 70-79 | 16 | 14 | 14 |
| 60-69 | 8 | 8 | 9 |
| 50-59 | 9 | 10 | 12 |
| 40-49 | 11 | 11 | 5 |
| 30-39 | 2 | 4 | 5 |
| 20-29 | 3 | 2 | 2 |
| 10-19 | 1 | 1 | 1 |
| 0-9 | 1 | 0 | 2 |
Table 2: Test Suite 2 (40 Hidden Nodes, 50 Input Nodes)
4.1 Does it learn better ?
Looking at the results of the experiments, it is quite obvious that both the serial and parallel evolved MLP learn better than the regular MLP. However, when we look more critically into the test suites, it becomes evident that in all cases except cases 2 and 3 the evolved perceptron does not actually help the neural network learn classifiers the regular MLP could not.That is the sum of tests that produced a success rate above 50 did not change across all MLPs. Although it is noticeable that the evolved MLP tends to produce more success rates above 90 than the regular MLP. Therefore, can we still say this algorithm learns better ? Yes we can still say this, because for the classifiers that all versions of the MLPs are able to learn, the evolved MLPs usually learn them better,thus producing more success rates above 90 than the regular MLP. However we cannot say that the evolved MLP algorithm helps the artificial neural network learn more, in the sense that it still cannot now learn new classifiers that the regular MLP could not.
4.2 Does it learn faster?
Since we have been able to establish that the evolved MLP algorithm learns better than your regular MLP using the test suites, the next question to ask is whether it learns faster than the regular MLP. Looking at table 6, it is quite evident that it learns faster as well. For instance, the first test where 5 input nodes were used and 4 hidden nodes, the regular perceptron takes quite a bit of time to finish learning all the classifiers.
| Accuracy % | Regular MLP | Serial Evolved MLP | Parallel Evolved MLP |
|---|---|---|---|
| 90-100 | 43 | 46 | 49 |
| 80-89 | 20 | 13 | 13 |
| 70-79 | 11 | 13 | 10 |
| 60-69 | 10 | 10 | 12 |
| 50-59 | 4 | 6 | 5 |
| 40-49 | 3 | 4 | 2 |
| 30-39 | 4 | 4 | 6 |
| 20-29 | 4 | 2 | 2 |
| 10-19 | 0 | 1 | 1 |
| 0-9 | 1 | 1 | 0 |
Table 3: Test Suite 3 (90 Hidden Nodes, 100 Input Nodes)
| Accuracy % | Regular MLP | Serial Evolved MLP | Parallel Evolved MLP |
|---|---|---|---|
| 90-100 | 48 | 48 | 48 |
| 80-89 | 13 | 13 | 14 |
| 70-79 | 6 | 6 | 4 |
| 60-69 | 5 | 4 | 6 |
| 50-59 | 3 | 4 | 3 |
| 40-49 | 4 | 3 | 4 |
| 30-39 | 15 | 15 | 15 |
| 20-29 | 2 | 2 | 2 |
| 10-19 | 2 | 4 | 2 |
| 0-9 | 2 | 1 | 2 |
Table 4: Test Suite 4 (452 Hidden Nodes, 500 Input Nodes)
| Accuracy % | Regular MLP | Serial Evolved MLP | Parallel Evolved MLP |
|---|---|---|---|
| 90-100 | 44 | 44 | 45 |
| 80-89 | 10 | 10 | 9 |
| 70-79 | 12 | 13 | 12 |
| 60-69 | 9 | 10 | 10 |
| 50-59 | 10 | 8 | 9 |
| 40-49 | 4 | 4 | 3 |
| 30-39 | 4 | 4 | 5 |
| 20-29 | 5 | 4 | 4 |
| 10-19 | 1 | 2 | 2 |
| 0-9 | 1 | 1 | 1 |
Table 5: Test Suite 5 (952 Hidden Nodes, 1,000 Input Nodes)
N/H=Number of Input nodes/Number of Hidden nodes
| N/H | Regular MLP | Serial Evolved MLP | Parallel Evolved MLP |
|---|---|---|---|
| 5/4 | 41 | 0 | 0 |
| 50/40 | 4 | 4 | 4 |
| 100/90 | 19 | 17 | 20 |
| 500/452 | 538 | 534 | 529 |
| 1000/952 | 2220 | 2104 | 1996 |
Table 6: Graph showing speed up between time taken measured in seconds and the Input Nodes/Hidden Nodes
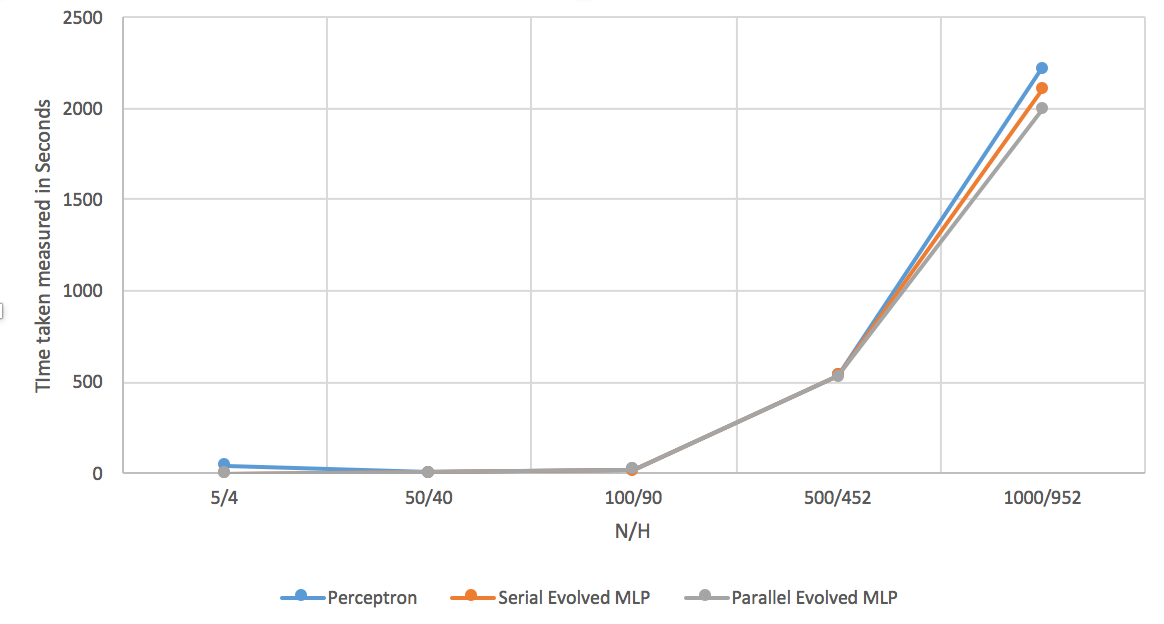
Perhaps why it could not learn just as quickly as the evolved MLPs is because there were some nodes that had very high prediction errors at the beginning and to get the network to learn those nodes needed to be corrected several times. However, following the evolved MLP algorithm, these nodes would simply be discarded as soon as the network deems them a liability and replaced with better ones, thus why it takes a significantly less amount of time.
However, looking at the results for parallel evolved MLP versus the serial evolved MLP, the parallelization did not seem to achieve any substantial amount of speed up. This may be because, the tests never get to a large enough input size that allows the cost of parallelization and synchronization to be insignificant in the face of the amount of computation needed. Perhaps using a larger amount of inputs would’ve shown how well the parallel version handles even larger data than 1,000 input nodes compared to the serial version. However, I feel as though more research needs to be done to improve the parallel version of the evolved MLP algorithm, and perhaps using a different parallelization structure such as MPI(Message passing interface) may have helped the situation more, but this is not certain for now. Overall the serial version of the evolved MLP performed better than expectation, but the performance of the parallel version was severely subpar.
Conclusion
The perceptron, albeit somewhat dated is still very much in use today, by several people and in several major projects. This paper is geared towards providing such people and projects with an improved version of the perceptron that gives them a faster and more “educated” artificial neural network. In this paper, we have discussed this new approach to the perceptron learning model, which is termed; the evolved perceptron. We were able to show that the evolved multilayer perceptron learns better and faster than the regular multilayer perceptron, when taught with the same data. We also looked into some methods of parallelizing this algorithm to make it even faster, and possible learn better, however this part of the experiment performed under expectations. The parallelized version of the algorithm did not achieve any substantial speed up as shown in figure 1. Hence, if this paper has provided any insight in regards to the parallelization of this new algorithm, it is to show what has been done unsuccessfully, and to show what could potentially be improved.
Future Work
Although this algorithm is already somewhat better than the regular multilayer perceptron, I believe a lot could be gained from the parallelization of this algorithm not just in speed but in its learning capacities. For instance, with the parallelization of the algorithm, when a node is replaced, each thread or process could replace it within its context and have somewhat of a competition among all the new nodes generated to see which one is the fittest; that theoretically could make the network learn better and more efficiently. More research however should be done into selecting the best parallelization structure, that will produce the least amount of overhead and increase the speed up, per proces-sor added. Since we have seen how much this basic addition of the survival of the fittest concept has added to the learning process, my next thought however is to see what other neuro-evolutionary concepts could be added to the regular multilayer perceptron to improve it.
References
- [Alsmadi et al., 2009] Alsmadi, M., Bin Omar, K., Noah, S., and Almarashdah, I. (2009). Per-formance comparison of multi-layer perceptron (back propagation, delta rule and perceptron) algorithms in neural networks. In Advance Computing Conference, 2009. IACC 2009. IEEE International, pages 296–299.
- [Karapetsas, 2009a] Karapetsas, L. (2009a). Multi-layer perceptron tutorial.
- [Karapetsas, 2009b] Karapetsas, L. (2009b). Perceptron neural network tutorial.
- [Lehman and Miikkulainen, 2013] Lehman, J. and Miikkulainen, R. (2013). Neuroevolution. Scholarpedia, 8(6):30977.
- [Stanley and Miikkulainen, 2002] Stanley, K. O. and Miikkulainen, R. (2002). Evolving neural networks through augmenting topologies. Evolutionary Computation, 10(2):99–127.
- [Wikipedia, 2004] Wikipedia (2004). Perceptron — Wikipedia, the free encyclopedia. [Online; accessed 9-Dec-2015].



